Equilibrium

A body is truly in equilibrium when it has no tendency to turn or move. This means no translation and no rotation.

When a body is in equilibrium:


and also:




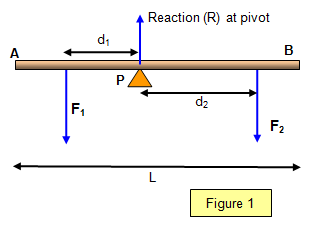
It is easy to show this using the light loaded beam of length L shown in Figure 1. Notice that F₁ will turn the beam anticlockwise about the pivot (P) while F₂ will turn it clockwise.

Using the principle of moments and taking moments about the pivot:
Balancing the vertical forces:


Notice the minus sign since R acts in the opposite direction from F₁ and F₂.

Further example

A more complex example where there are three forces acting on the rod is shown below (Figure 2). The rod is pivoted about its centre.




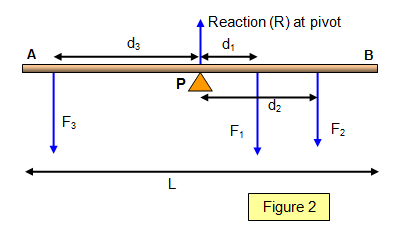
Using the principle of moments and taking moments about the pivot:
Clockwise moments = F₁d₁ + F₂d₂ = F₃d₃ = Anticlockwise moments

Moments may be taken about any point

(a) If we take moments about end A :

Anticlockwise moments = LR/2 = [L/2 + d₁] F₁+ [L/2 + d₂] F₂ + [L/2 – d₃] F₃ = Clockwise moments

(b) If we take moments about end B :

Anticlockwise moments = [L/2 - d₁] F₁+ [L/2 - d₂] F₂ + [L/2 + d₃] F₃ = LR/2 = Clockwise moments

Combining equations (a) and (b) gives:

Clockwise moments = F₁d₁ + F₂d₂ = F₃d₃ = Anticlockwise moments

This is the identical result that we obtained by taking moments about the pivot.