Friction between solids

Life as we know it would he very strange without friction. Friction is useful in brakes - indeed, without the frictional force between our feet and the ground we could not walk! Frictional forces play a large part in the losses of energy from machinery and in this area great efforts have been made to reduce them. Guillaume Amontons first established that there existed a proportional relationship between friction force and the force between the bodies in contact. Amontons' paper 'De la résistance causée dans les machines' was published in 1699 in Memoires de l'Académie des Sciences.

To move one body over another which is at rest requires a force. This is needed both to change the momentum of the first body and also to overcome the frictional force between the two surfaces. The force needed to overcome the frictional force when the bodies are at rest is called the limiting friction.
By experiment it has been found that the limiting frictional force between two surfaces depends on
(a) the nature of the two surfaces, and
(b) the normal reaction between them. This can be expressed as an equation as

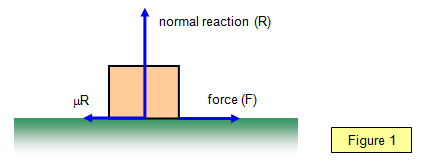
frictional force (F) = coefficient of friction (μ) x normal reaction (R) (Figure 1)

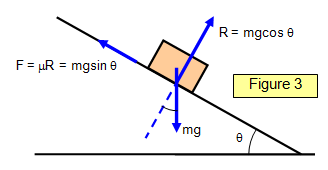
The coefficient of friction depends on both surfaces.

When the object is moving the friction between the two surfaces is usually less than the limiting friction. It is known as the coefficient of kinetic friction and is almost independent of the relative velocities of the two surfaces.

Coefficients of friction:

Materials	Static	Kinetic
Steel on steel	0.74	0.57
Aluminium on steel	0.61	0.47
Copper on steel	0.53	0.36
Brass on steel	0.51	0.44
Zinc on cast iron	0.85	0.21
Copper on cast iron		0.29
Glass on glass	0.94	0.4
Copper on glass	0.68	0.53
Teflon on teflon	0.04	0.04
Teflon on steel	0.04	0.04
Steel on air	0.001	0.001
Rubber on dry concrete	1.0	0.8
Rubber on wet concrete	0.3	0.25
Steel on ice	0.03
Tendon and sheath	0.013	0.8
Lubricated bone joint	0.001	0.003
Wood on wood	0.3
Waxed wood on dry snow		0.4
Waxed wood on wet snow		0.1

You will see later that it is very simple to calculate the coefficient of friction from the slope down which an object will slide. Remember that a frictional force always acts to oppose the motion.

The frictional forces between glass fibres and the resins in which they are embedded (fibre-glass) are vital factors in the strength of these materials.

Careful study of friction has shown that the frictional force between two surfaces is independent of the area of contact. This can be explained as follows.

Think of two surfaces of steel which have been polished. When they are placed together we think that they are in contact over their whole surface area but this is not the case.

In fact, they only touch at something like one ten-thousandth of their actual area as shown in Figure 2.

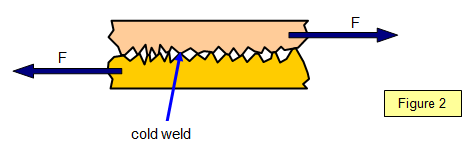
At the points of contact the surfaces are actually cold-welded' together and it requires energy to break the welds.

The motion of the top surface over the other is a stick-slip movement: the small projections have to be broken as the object moves.

The friction between a rubber tyre and the surface of a road is of considerable importance in safety. In normal use the tyres have a tread to allow the passage of water but in dry racing-car tyres, the so-called 'slicks', the tyre is perfectly smooth and relies on the heat generated due to friction to melt a little of the tyre and so increase the road-holding ability.

Measurement of the coefficient of friction between two solid surfaces

(i) Direct method
A mass A is pulled across a horizontal surface by a Newton-meter and the force required is recorded. If the weight of the object is known, the coefficient of friction may be determined.

(ii) Using a slope
The object is placed on a slope as shown in Figure 3 and the tilt of the slope (θ) is slowly increased until the object begins to slide down.

At the moment of slip the forces on the object are given by:

along the plane: F = mg sin θ
perpendicular to the plane: R = mg cos θ

Therefore:

Coefficient of friction (μ) = F/R = tanθ