Pressure in compressible fluids
In working out the pressure at a given depth in water we assume that the
water is incompressible – that is its density is constant with depth. This is very nearly
accurate. However this would not be true of a fluid such as air. In the atmosphere the
pressure increases with depth but the density of the air also varies from 1.2 kgm-3
at sea level to virtually zero at the edge of space.
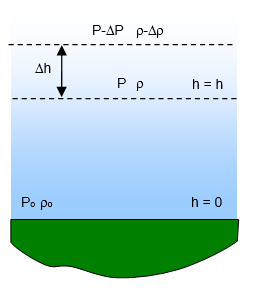
Let the change in pressure due to a small change of height Δh be Δp
Take the density at a height h to be ρ and the density at the height h+Δh to be
ρ-Δρ.
If the temperature (T) of the air is constant ρ is directly proportional to the pressure (p)
and so:
p/po = ρ/ρo
where po and ρo are the pressure and density of air at
sea level.
Therefore Δp/Δh = -
rg = -gρo[p/po]
When this is integrated we have:
Pressure (p) at a height h = poe-g[ρo/po]h
Density (ρ) at a height h = ρoe-g[ρo/po]h
Substituting for the
accepted values of g, p
o and
ro we have:
Pressure (p) at a height h = poe-0.116h
(N.B – the
height h should be given in kilometres here)
Example problem
1. Calculate the pressure of the air at a height of 10 000 m (10 km) (the height at which many intercontinental jets fly). Take the pressure at sea level to be 105 Pa.
Pressure (p) = 105e-0.116h
Pressure = 105xe-1.16 = 3.13x104 Pa or about a third of that at sea level.
2. Calculate the distance below the surface of the Earth at which a piece of iron (density 7870kgm-3) will float in air if the density of air at sea level is 1.3 kgm-3.
7870 = 1.3e-0.116h
Therefore 6053 = e-0.116h giving h = 75 km!
The temperature of the
atmosphere also decreases with height.
The standard variation being a drop of 6
oC for
every kilometre above the ground up to 11 km. After that it remains constant at around – 55
oC.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB