
The forces in the hinges of a door is a useful demonstration of three
vectors in equilibrium.
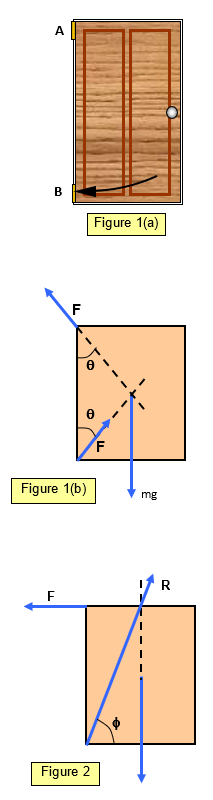
Figure 1(a) shows a door and the forces on the door are shown in
Figures 1(b). (For simplicity the door is shown as completely uniform)
The hinges (A and
B) are symmetrical, placed at the corners of the door and each supports half the weight of the
door. The forces (F) in each hinge are equal.
To understand in which direction
the forces on the door we must appreciate the following:
(a) the three forces on the door
are
(i) its weight (mg)
(ii) the force due to hinge A
(iii) the force due to hinge B
(b)
what happens if one or other of the hinges are disconnected from the door
(i) if hinge A is
disconnected from the door the door will tip downwards and away from the frame (direction a in
Figure 1(a)
(ii) if hinge B is disconnected from the door the door will tip downwards and
inwards towards the frame (direction b in Figure 1(a)
This means that the force of hinge A is upwards and towards the frame and
the force of hinge B is upwards and away from the frame. (See diagram 1(b).)
Resolving
the forces on the door vertically we have: