Vectors in equilibrium
For an object to be in equilibrium the following two
conditions must be satisfied.
The sum of the moments of the forces on the object about any point must be zero.
The resultant of the forces on the object in any direction must be zero.
It
follows from the first condition that if three non-parallel vectors (such as forces) act in an object
that is in equilibrium then the lines of action of these three vectors must pass through one point.
The vectors can be represented in magnitude and direction by the three sides of a
triangle – the vectors must be drawn so that their direction follows round the
figure.
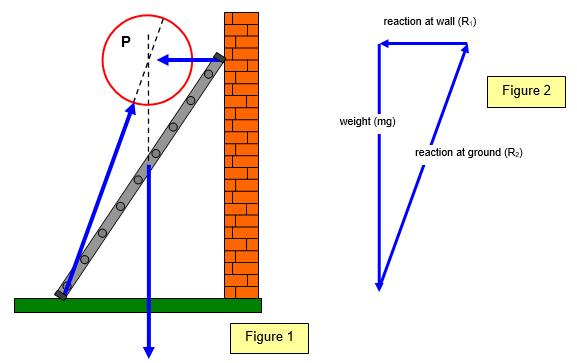
Vectors in equilibrium Ladder
A good example of the case of
vectors in equilibrium is a ladder resting on rough ground and leaning against a smooth wall - see
Figure 1.
Notice that the three forces involved are:
(a) the weight of the ladder
(b) the
reaction at the wall (R1) – at right angles because the wall is smooth
(b) the reaction at the
ground (R2) - not at right angles as the ground is rough
and that they all pass through the
same point P.
The vector diagram for the three forces involved is shown in Figure 2.
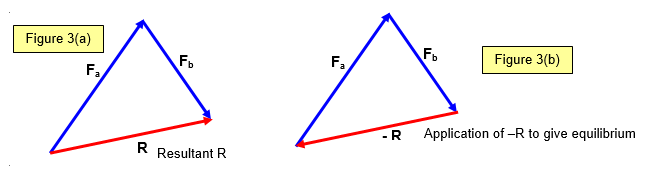
If two forces (Fa and Fb) act on
an object (Figure 3(a)) then if the reverse of the resultant (R) is applied to the object as well the
system will be in equilibrium (Figure 3(b)).
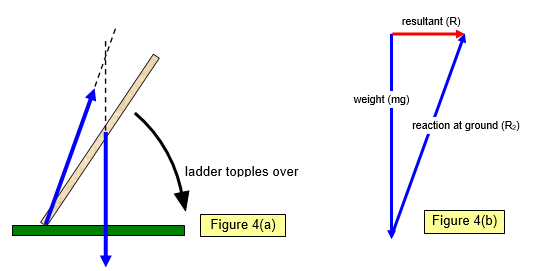
Now returning
to the case of the ladder.
If the wall is suddenly taken away there are only two forces acting
on the ladder – its weight and the reaction at the ground. These two would give a resultant R and
the ladder would topple over to the right (Figures 4(a) and (b). Applying the reverse of R (putting
back the wall) and making sure that all three forces passed through the same point would hold the
ladder in place again.
Two
versions of the ladder problem are now considered. The first using only the resolution of vectors
and the second using moments and the resolution of vectors.
Example problem (version 1)
A ladder with a mass of 15 kg stands on rough ground and leans against a smooth vertical wall. The reaction at the ground acts at an angle of 20o to the vertical.
Calculate:
(a) the size of the reaction (R2) at the ground
(b) the size of the reaction at the wall (R1)
(Assume that the reaction at the wall acts at 90o to the wall)
(Take g = 9.8 ms-2)
Weight of the ladder = mg = 15x9.8 = 14.7 N
(a) Resolving the forces vertically mg = R2cos20 and so R2 = 14.7/0.94 = 15.6 N
(b) Resolving the forces horizontally R1 = R2sin20 and so R1 = 15.2xsin20 = 5.35 N
Example problem (version 2)
A ladder 3 m long with a mass of 12 kg stands on rough ground and leans against a smooth vertical wall at an angle of 16
o to the vertical. (Figure 5)
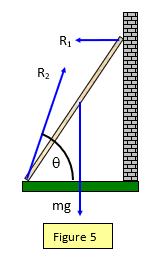
Calculate:
(a) the size of the reaction at the wall (R
1)
(b) the size of the reaction (R
2) at the ground
(Assume that the reaction at the wall acts at 90
o to the wall) (Take g = 9.8 ms
-2)
(a) Take moments about the base of the ladder
Anticlockwise moments = R
1x3xcos16 = Clockwise moments = mgx1.5sin16
Therefore: R
1 = [12x9.8x1.5x0.28]/[3x0.96] = 48.62/2.88 = 16.9 N
(b) Let R
2 make an angle of θ with the vertical
Resolving vertically: R
2cosθ = mg
Resolving horizontally: R
2sinθ = R
1 = 16.9
Therefore: tanθ = 16.9/[12x9.8] = 0.143 θ = 8.2
o
and so: R
2cosθ = mg R
2 = 12x9.8/cos8.2 = 119 N
R
2 can also be found using Pythagoras’ theorem when R
1 is known.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB