THE CYCLOTRON

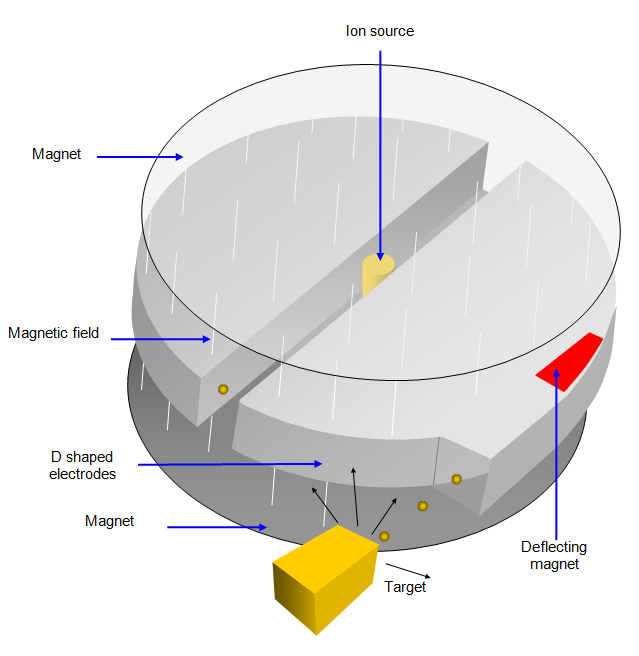
In 1932 an American Physicist, Ernest Lawrence devised a different type of accelerator which he called the cyclotron. Built in 1934 by E.O Lawrence and M.S Livingstone. This machine was circular, the first one only a few centimetres across, he later built one with a diameter of 1.5 m. A simple drawing of a cyclotron is shown below.

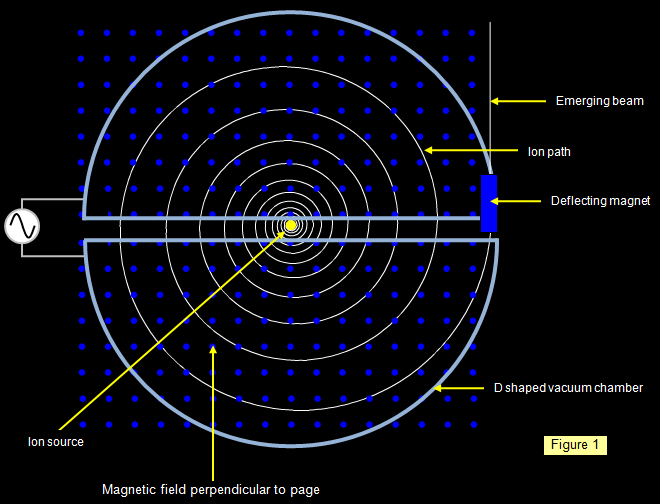
It is basically a circular evacuated chamber cut into two D shaped halves with a high voltage (V) across the gap. The particles are injected at the centre and a magnetic field (strength B) is applied across the whole of the apparatus perpendicular to the Ds so that the particles are deflected into a circular path.

They start at the centre and are given a kick every time they cross the gap between the Ds. The energy gain is qV for ions of charge q. As they gain energy from the electric field their velocity increases and so the radius of their path increases. This meant that they travel in an ever growing spiral until they emerge at the edge of the apparatus and hit a target.
The maximum kinetic energy of the particles when they leave the Ds is:





where R is the radius of the Ds.

It is interesting to consider the frequency of the accelerating voltage as the energy of the particles gets greater.

Centripetal force on the particle = mv²/R = m4p²R²/T²R = m4p²R/T² = Bev
So Bev = mv²/R and therefore v = BeR/m
Frequency = 1/T = v/2pR = [BeR/m]/2pR = Be/2pm and this is independent of the orbit radius and is constant for fixed field, charge and mass.



However at particle energies above about 20 MeV relativistic effects become a problem as the increase in mass of the particle becomes significant.

One disadvantage of this apparatus was that the energy was limited by the size of the machine and the magnetic field. Each particle could only make one spiral. Another disadvantage is that the magnetic field must cover the whole of the apparatus and all the space between the Ds must be evacuated.