Energy in a
hanging rope
Consider a rope of mass m, natural length L and modulus E where k
= E/L.
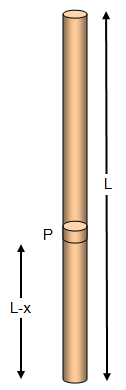
Suppose a point P is at a distance x from the top before extension.
Length of
rope below P when unstretched = L-x
Weight of rope below P when unstretched = [L-
x]/Lmg
And this will accordingly be the tension at P when the rope is
suspended.
Now consider an element of length δx at P,
and suppose the extension of this element is e.
Then we have: ([L-x]/L)mg =
Ee/δx x
Therefore energy of the element =
Ee
2/2δx x = ([(L-
x)
2m
2g
2]/2EL
2) δx
x
The total energy in the hanging rope is the integral of this from 0 to L.
Total energy = m2g2L/6E =
m2g2/6k
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB