
The most simple form of variation of the extension of an object when a force is applied is known as Hooke's Law, proposed by Robert Hooke, the founder of the Royal Society, in 1676. He showed that:
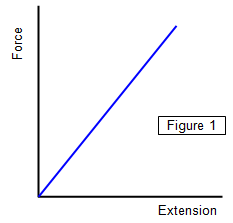
This shows that the extension is directly proportional
to the applied force – doubling the force will double the extension. If a graph of force is
plotted against extension a straight line will be obtained (Figure 1).
Note: Hooke’s law is only valid if the elastic limit of the material is not exceeded.
This is the kind
of graph that you would get if you loaded a helical spring or a copper wire as long as you
kept the loads fairly small. Where F = ke a molecule displaced from its original position (by
squashing or stretching the material) will try and return to its original position. If released it
will oscillate about that position with simple harmonic motion.
The constant k is
known as the elastic constant for the material and is defined as F/e. The units for k are Nm-
1.