The extended half-life of fast moving muons – time dilation

Before reading this have a look at the file called 'Time dilation'. Effects similar to those described there have been observed in the real world, but because of the very large velocity of light they are much more difficult to see.

The slowing down of time (time dilation) has been noticed in atomic clocks that have been carried in satellites but a natural phenomenon that supports time dilation is the decay of fast moving muons as they travel downwards through the atmosphere.

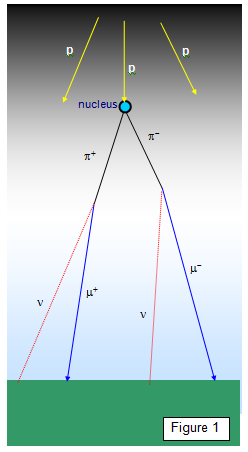
High-energy cosmic ray protons entering the upper atmosphere interact with the nuclei of oxygen and nitrogen atoms to give a group of pions and these then decay into muons that then move off at a speed of up to 0.994 c. These muons are formed at a height of between ten and fifteen thousand metres above the ground.

The half-life of a muon is 2.2 microseconds and so even moving at 0.994 c they would only expect to travel about 660 m before half of them decayed. Muons formed at, say 12000 m would take 40 <μs or about 20 half lives to reach the ground. This would mean that only 1/2²⁰ of the original number would be detected. The fact that the proportion is much higher than this means that the muons are living longer.

At 0.994c the formula for time dilation gives the half-life for the muons to be 20 μs. This means that at 0.994c the proportion reaching the ground should be 0.25. This means that the number of muons per second detected at the ground is much greater than expected.

(Note: in Figure 1 only pion decays that result in muons are shown. A μ_o decays resulting in gamma rays, electrons and positrons are omitted)

Mass increase with velocity and the 'cosmic speed limit'
The increase of mass becomes a problem in high-energy accelerators where as the particles approach the speed of light they become more and more difficult to accelerate further. Even the electrons in our colour television tubes are moving so fast that their actual masses are some 21 per cent heavier than those of electrons at rest. Beta particle emitted in radioactive decay are moving at 90% of the speed of light and are 2.4 times heavier than an electron at rest.

Using the formula for the relativistic mass of a particle you can see that there is kind of cosmic speed limit for matter.

Since: m = m_o/(1 – v²/c²)^1/2 close to that of light the mass of a particle becomes very high and at v = c the limit of further increase in speed is reached. The mass of the particle is converted into energy.

Relativistic velocity addition

If two objects are moving relative to each other the maximum relative speed allowed by the special theory of relativity is the speed of light (c). The equation for the addition of relativistic velocities (ones where relativity would become important) is:

Relativistic velocity addition: Relative speed = [v_A + v_B]/(1 + [v_A x v_B]/c²)

Where v_A and V_B are the velocities of the two object relative to some external reference frame (v_A and v_B are both less then the speed of light).

Two photons approaching each other

A further consequence, and indeed a requirement of special relativity, is the fact that the velocity of light in free space is constant. This means that the relative velocity of two photons approaching each other in free space, when measured from one or the other, is c and not 2c.
This can be proved using the formula for relativistic velocity addition:

Relativistic velocity addition for two bodies moving at speeds v_A and v_B relative to an external reference frame:
Relative speed = [v_A + v_B]/(1 + [v_A x v_B]/c²)

For the two photons v_A = v_B = c and so
Relative speed = [c + c]/(1 + [c x c]/c²) = c

However this is different if you are in a frame of reference outside both photons and observing them approaching each other. You now observe the approach velocity to be 2c. This does not contradict the special theory of relativity because neither photon is moving faster than the speed of light (c).

The equivalence of mass and energy

You have probably used Einstein's famous equation relating matter to energy, E = mc². This equation can be deduced starting with the first equation of special relativity:
(See: Mass energy equation)

Light beam to the Moon – a paradox or not

Imagine an experiment where you shine a laser beam onto the surface of the Moon so that the beam hits one edge of the visible disc. Now swing the laser through an angle of 0.5^o, the angle subtended by the Moon at the Earth, in 0.01 s. This would mean that the beam would have travelled across the lunar surface – a distance of 3 500 000 m. This means that the beam is moving across the Moon's surface at 3500000/0.01 = 3.5x10⁸ ms^-1.

There is no problem here – the result does not contradict the theory of relativity. No individual photons make that traverse since as the beam moves different photons arrive at different places.