
Using apparatus devised by Lummer and
Pringsheim the energy emitted by a black body may be measured over a range of different
temperatures and in many different regions of the spectrum. The results obtained can be
summarised as follows.
(a) the total energy (E) emitted by a black body per unit area per
second is proportional to the fourth power of the absolute temperature (T) of the body. This is
known as the Stefan-Boltzmann Law.
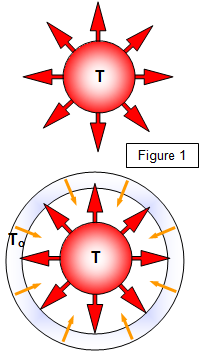
(b) if the temperature of the body's surroundings are at a temperature To there will be an exchange of heat energy between them and the body. The net loss of energy from the body per unit area becomes:
(d) the nature of the surface is allowed for by a quantity known as the emissivity (ε) - for a black body this is equal to 1 and for all other surfaces it is <<1. The equation for the net loss of energy per second now becomes:
It is important to realise the difference between this equation and Newton's law of cooling. Stefan's law applies to the loss of energy by radiation while Newton's law applies to loss of energy by convection. Both laws are found to hold for temperature differences of hundreds of degrees.