Conduction of heat energy
The transfer of heat energy from one place to
another through a substance without the movement of the substance as a whole is known as
conduction.
Conduction of heat is most important in the insulation of houses because much
of the heat produced in the house is lost by conduction through the walls, roof, windows and
floor and knowledge of materials that can be used to reduce this loss is of great importance.
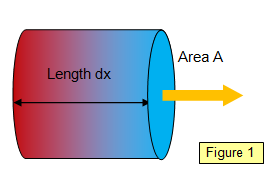
If we consider a specimen of
length dx and cross-sectional area A, with a temperature difference d
q between the opposite faces (Figure 1), then the rate of flow of heat
energy through it will depend on
(a) the cross-sectional area of the face, (A)
(b)
the temperature difference between the faces (dθ)
(c)
the inverse of the distance between the faces (1/dx)
Therefore:
Rate of flow of heat: dH/dt = -kA[dθ/dx]
where k is a constant known as the
thermal conductivity of the material, measured in W m
-1 K
-1.
The thermal conductivity is defined as rate of flow of heat between two surfaces of unit area separated by unit distance when the temperature difference between them is 1 K
(Notice the negative sign: this implies that the
temperature will decrease as the distance down the bar increases). Notice also that you may
use oC or K for the units for temperature difference. The actual temperature is not
vital – simply the difference in temperature between the two faces. The value of k for various
materials is given in the table below (see Data section for further values).
| Material |
k(Wm-1K-1) |
|
Material |
k(Wm-1K-1) |
|
Material |
k(Wm-1K-1) |
| Silver |
419 |
|
Copper |
385 |
|
Chlorine |
0.007 |
| Aluminium |
200 |
|
Iron |
80 |
|
Air |
0.024 |
| Glass |
0.8 |
|
Brick |
0.6 |
|
Meths |
0.20 |
| Wood |
0.15 |
|
Cork |
0.05 |
|
Water |
0.59 |
Student investigation
You may have performed a simple experiment in your GCSE course to investigate the conductivities of various metal rods by holding one end of them in a bunsen flame and seeing which one you have to put down first when it becomes too hot to hold. How much of this effect is due to the thermal conductivity of the specimen and how much to the rate at which the specimen can be warmed up, that is, to its specific heat capacity?
Use a thermocouple and a data logger to investigate the rate of rise of temperature at different points along a metal rod when one end is placed in a bunsen flame. Plot a graph of temperature against time and attempt to deduce the form of the equation relating these two quantities. Try different metals, and also specimens with different cross-sectional areas.
How would lagging the rods affect your results?
WORD VERSION AVAILABLE ON THE SCHOOLPHYSICS CD