
All optical instruments give
images that are affected by the diffraction at the objective lens, so if we have two points on the
object that are close together it is possible that their images may possess diffraction patterns
that will overlap. If they are too close the images of these two points will be indistinguishable
from one another. This is especially important in astronomy where the images of two stars that
are very close together need to be separated. The aperture of the telescope needs to be as
large as possible to give as little diffraction as possible.
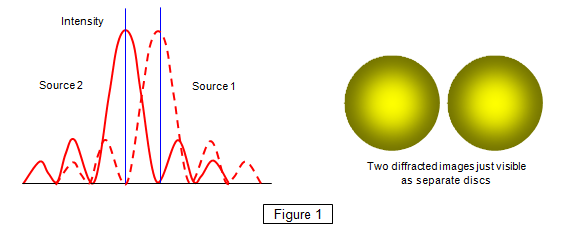
For two images of equal
intensity to be resolved the central maximum (constructive interference – maximum brightness)
of one diffraction pattern must fall no closer than the first minimum (destructive interference –
darkness) to the centre of the second diffraction pattern (Figure 1). Using the formula for a
rectangular aperture we have:
You can see that higher resolution is possible with large apertures or with short-
wavelength radiation such as ultraviolet light, X-rays or even electrons. The same problem
occurs with microscopes – there is no point in magnifying an image greatly if all you are doing is
magnifying two overlapping diffraction patterns. This is why ultra violet light or electrons are
used in microscopes where a very high magnification is needed.
The eye can resolve
fine detail rather better if the lighting is not too strong, so that the pupil will have a large
aperture.
The problem with very large optical telescope mirrors has been overcome to some extent by the use of multiple mirror telescopes. These instruments use a number of smaller mirrors mounted to give the same light-gathering power and resolving power as a very large single mirror.
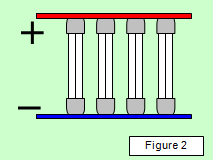 The resolving power of a system may be studied by the following simple experiment. Set up a multiple light source (Figure 2) and view it through a single adjust-able slit in front of which is a green filter. Observe the change in the appearance of the source as the width of the slit is changed.
The resolving power of a system may be studied by the following simple experiment. Set up a multiple light source (Figure 2) and view it through a single adjust-able slit in front of which is a green filter. Observe the change in the appearance of the source as the width of the slit is changed.