Newton's rings
This
method for determining the wavelength of light was proposed by Sir Isaac Newton in his book
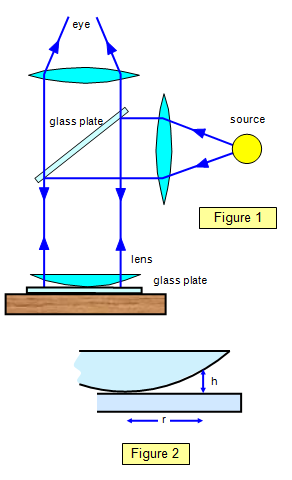
Opticks, published in 1717. The experimental arrangement is shown in Figure 1.
A
plano-convex lens of large radius of curvature R is placed on a plane glass plate with its curved
surface downwards and is illuminated from above with a parallel beam of monochromatic light.
Some of the light is reflected from the upper surface of the glass plate and some from the lower
surface of the lens; interference thus occurs by division of amplitude, the fringes being localised
in the air gap between the lens and plate.
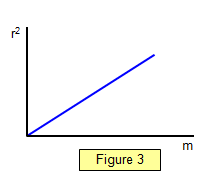
At any point a distance r from the axis of the
lens the path difference will be 2h, where h is the distance between the lens and the plate at
that point (See Figure 2). The interference fringes are circular because the system is
symmetrical about the centre of the lens. The radius of any ring is given by:
(2R - h)h =
r2 so r2 = 2Rh – h2
But h2 is small compared with 2Rh
and so: 2Rh = r2
The path difference (2h) is therefore r2/R
A phase change of π occurs when the light reflects from the top surface of the plate but
not at the lower surface of the lens, and therefore:
For a bright ring viewed by reflection: (2m + 1)λ/2 = rm2/R
For a dark ring viewed by reflection: mλ = rm2/R
where m = 0, 1, 2, 3, etc and r
m is the radius of the m
th ring.
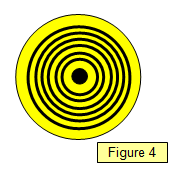
If a graph is
plotted of r
2 against m for the dark rings a straight line should be produced with a
gradient given by:
(r
m2 - r
12)/(m - 1) = λR
where r
1 and r
m are the radii of the first and m
th rings respectively. (See Figure
3).
When doing the experiment it is much easier (and more accurate) to
measure the diameter of the rings and then calculate their radius. A dark central spot should be
obtained when viewed by reflection.
The
rings can be viewed by transmission by putting the microscope below the plate, and if this is
done the equations for bright and dark rings should be interchanged as two phase changes will
occur, producing an effective phase difference of 2π. A bright central spot should be
obtained.
If white light is used a few coloured rings will be seen due to the different
wavelengths of the different colours of light.
Newton's rings and the
refractive index of a liquid
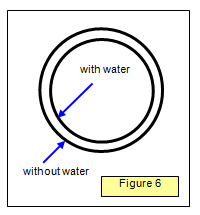
Putting a liquid of refractive index n between the
lens and the plate (Figure 5) will change the path difference to 2nh and give a formula for the m
th dark ring of:
mλ = [nrm2]/R
The radius of any
given ring will be less with the liquid in place than without it.
This effect may be used to
measure the refractive index of the liquid; the method is a good one since it is accurate and
easy to perform, and only a small amount of the liquid is needed.
 Example problem
Example problem
Calculate the ratio of the diameters of the fifth interference rings with and without water (refractive index 1.33) between the lens and the plate if the radius of curvature of lens is 0.50 m.
Without water:
r
m2 = R
m= 0.5x5 xλ
With water:
r
m2 = R
ml/n = [0.5x5xλ]/1.33
Therefore:
ratio of radii = 1/(1.33)
1/2 = 0.87
Example problem
A series of rings formed in Newton's rings experiment with sodium light was viewed by reflection. The diameter of the mth dark ring was found to be 0.28 cm and that of the (m + 10)th 0.68 cm. If the wavelength of sodium light is 589 nm, calculate the radius of curvature of the lens surface.
For the mth ring: [(0.14x10-2)2 ]/R = mx589x10-9
and for the (m + 10)th ring: [(0.34x10-2)2]/R= (m + 10)
where R is the radius of curvature of the lens surface.
Therefore:
0.342/0.142 = (m + 10)/m giving m = 2.
Therefore, substituting for m, R = 1.66 metres.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB


 If a graph is
plotted of r2 against m for the dark rings a straight line should be produced with a
gradient given by:
If a graph is
plotted of r2 against m for the dark rings a straight line should be produced with a
gradient given by:

 Example problem
Example problem