
A stationary or standing wave is one in which the amplitude varies
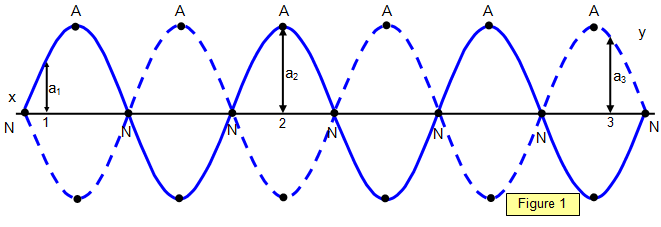
from place to place along the wave. In a standing wave some points along the wave are stationary, while others vibrate with amplitudes up to the maximum for that wave.Figure 1 is a diagram of a stationary wave. Note that
there are places where the amplitude is zero and, halfway between, places where the
amplitude is a maximum; these are known as nodes
(labelled N) and antinodes (labelled A) respectively.
(See
Figure 1)
The distance between successive
nodes, and successive antinodes, is half a wavelength. (λ/2)
The amplitude of the
points on a stationary wave varies along the wave. In Figure 1 the amplitude at point 1 is
a1, that at point 2 is a2 and that at point 3 is a3. The displacement (y) at
these points varies with time.
Any stationary wave can be formed by the addition of
two travelling (progressive) waves moving in opposite directions.
A wave moving in one direction
reflects at a barrier and interferes with the incoming wave.

The standing waves on a string may be studied using an experiment due to Melde and shown in Figure 2(a). A 0.5 m long rubber cord of 3 mm2 cross-section is clamped at one end, stretched to twice its length and fixed to a vibrator. The vibration generator is connected to a signal generator which can give a range of frequencies between 10 Hz and 100 Hz.
Observe the effects of slowly increasing the vibrator frequency from 10 Hz to 100 Hz and explain what you see. The experiment is best done in a darkened laboratory with the cord illuminated with a stroboscope.

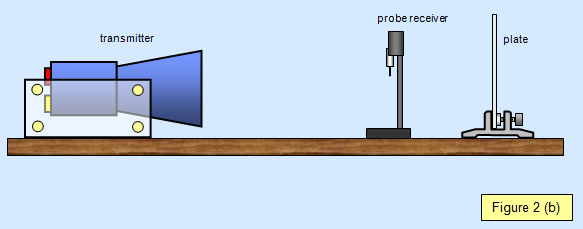
The transmitter is set up facing a vertical metal plate about 50 cm away. If a probe detector connected to a meter is moved along the line between transmitter and plate a series of nodes and antinodes can be found. The distance between successive nodes or antinodes is half the wavelength of the microwaves.