Cannons and satellite orbits
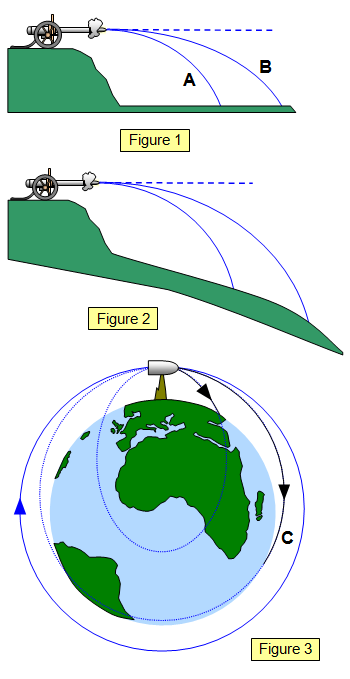
If a shell is fired horizontally from a cannon it will follow a parabolic path
until it hits the ground (Figure 1) – trajectory A. The faster the shell leaves the cannon the
greater the range, shown by trajectory B.
However, if the ground is sloping away
from the cannon then for a given muzzle velocity the shell will travel further before it reaches
the ground (Figure 2).
Now if we imagine the ground sloping away more and more
steeply the shell will go even further. Finally think of the Earth as a globe.
Take the
cannon to a mountaintop and fire the shell (Figure 3). The surface of the planet slopes away
from the cannon so the shell will curve downwards towards the ground (see trajectory C).
However if the shell is fired fast enough it will orbit the planet – 'falling' towards the centre of
the Earth all the time.
You can calculate the required muzzle velocity of the shell (v)
for an orbit at a given height from the equation:
F = mv2/(R+h) =
GMm/(R+h)2 = mg
Where R is the radius of the Earth, h is the height
above the ground and g is the acceleration of gravity at that height. In fact for satellites in low
altitude orbits h is probably going to be very small compared with R it can be ignored in a
rough calculation and g can be taken as that at the Earth's surface.
Therefore:
v2 = Rg
Given that the radius of the Earth is 6.4x106 m
and that g is 9.81 ms-2 we have:
Orbital velocity (shell muzzle
velocity)(v) = 7200 ms
-1.
This idea shows you that satellites not only
require to be put up a certain distance above the surface of the planet but also need a
tangential velocity. This process is called orbit injection.
The satellites can be put in
a variety of orbits and their velocities and periods will vary depending on their distance from
the Earth. Those closer to the planet will have the higher orbit velocities and shorter
periods.
The Russian satellite Sputnik 5 launched in 1960 orbited at a mean height
of about 306 km with a period of 90.7 minutes. This would have given it an orbital velocity of
7740 ms
-1.
Notice that this is larger than the rough estimate for a low level orbit given
earlier. The reason for this is that the earlier value assumed a circular obit and a spherical Earth while
the Sputnik orbit was actually elliptical and the values given are the actual parameters for the
orbit.
A communications satellite launched into an orbit of radius 42000 km would
have an orbital velocity of 3050 ms
-1.
Satellites can be launched into a
number of different orbits but the orbit must always be centred on the cent of the Earth.
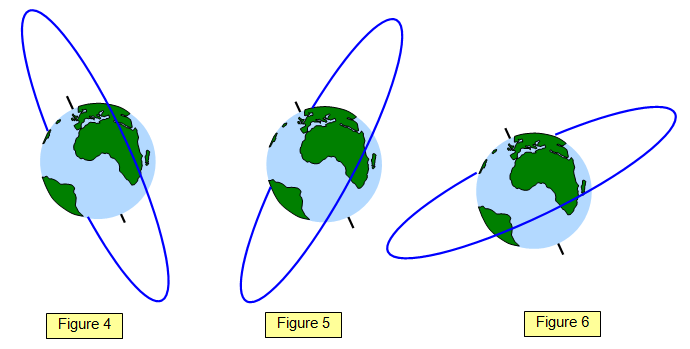
Satellites with orbits over the pole
(Figure 4) are said to have polar orbits.
Satellites with a period of one day are
known as geosynchronous satellites (Figure 5) while those with a period of one day and an
obit in the plane of the equator are geostationary – they will 'hang' over one point on the
planet (Figure 6). It is these that are used as communication satellites.
Note: the
diagrams are not to scale.
For further details of communication satellites see:
Geostationary satellites
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB